 This is my first attempt at a “Made 4 Math Monday” post. What follows is certainly making, and definitely math. I hope you enjoy!
This is my first attempt at a “Made 4 Math Monday” post. What follows is certainly making, and definitely math. I hope you enjoy!
The other day I tagged along with Paul when he went to NYC Resistor to laser cut a piece of mathematical art. For a while now, Paul’s been creating all kinds of amazing art that involves stars. That’s STARt, for short. He should really put up a gallery of his artwork on his blog. nudge, nudge.
Anyway, for this piece he was cutting all of the twelve-pointed stars out of plexiglass, planning to stack and glue them into a sculpture. There were of course some leftover scraps from the cutting, including 12 nice isosceles triangles that he passed on to me. They’re just the shape of triangle that you get when you pizza-slice a dodecagon.
After our outing, I was in an artsy mood and found myself playing with the triangles. I was amazed by how many ways of arranging them presented themselves to me, just by futzing around with them. It was a pleasant and exciting activity. Here are a couple of pictures I took of my creations:
Playing with the triangles got me thinking about some further patterns that I wanted to try out. Like: what would happen if I stuck the triangles together along their long sides in a chain, pointing up and down at random? What would the long-term behavior look like?
So I did some programming, first in Scratch and then in Processing. Here’s a short clip of what I’ve gotten to see so far. It’s given me food for thought about connections between this pattern and David Chappell’s meander patterns.
And if you tweak a few parameters–including weighting the probabilities as a function of the number of triangles that have been laid down–you can get something like this instead. Nice!
And so?
What I took away from this was how having unfamiliar and tangible mathematical objects around led to play and product and inquiry. This felt real and striking to me.
What does this mean for my classroom? I want my students to have experiences like these—open, creative, productive experiences with mathematical objects that they feel connected to. Having lots of accessible and flexible mathematical objects in the room is a good direction to head in.
Writing Math Munch is one way I try to expose my students to new objects, patterns, and structures, but now I’m vicariously craving really tangible math experiences for my students. This gave me the thought (a recurring one) of how I want there to be a superabundance of supplies in my room. I was in an art classroom at school earlier this week working on another project, and I was just so struck by how much stuff there is in that room. I want there to be stuff in my room, too—both clearly mathematical stuff and stuff that has the potential to be.
What do you make sure to keep around in your classroom for kids to have access to? Or would like to? There are some things I keep around, like pipe cleaners and twisty balloons and poster board; markers and protractors and geometry building tools (Zome, Geofix, pattern blocks). But I want more. Because I want my students to futz. Thoughts?
Hooray for making and math! #made4math
P.S. One final product of futzing: a further riff on STARt, inspired by Paul’s. Made of thread and a water bottle.


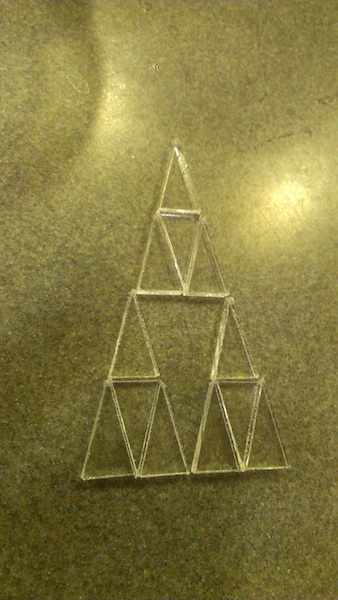






This post reminded me once again that the standard elementary school pattern block set is way too limiting. I love how playing with isosceles ‘blocks’ for instance totally changes one’s perception of what a triangle ‘is’. Anyhow, Paul has inspired me with his stars as well — I made an attempt at a lesson for my 7yo daughter using stars and posted about it on my blog.
I was just reading your star post! I love your blog–the photos and stories and all the personal meaning that is made.
Pushing past the limitations of prefabricated manipulatives–that’s a big part of what makes laser cutting and 3D printing so exciting. And I find that the design attitude prompted by having these heavy-duty technological tools around carries over to other things–I think about paper and scissors differently now than before. I feel like this is a little bit of a return to lost ways of thinking, for myself–that kids are often more comfortable with creating things than I am. I’m excited to find out what all will get made in my classroom this year!
A mishmash of thoughts. Thanks for bringing them out of me!
Can’t wait to see what is made in your classroom this year, too! My Math in Your Feet kids have been making math using percussive dance for years, but I never really knew anyone else who was doing that or even used those words. I’m glad my blog (and twitter and FB) have helped bring me out of isolation and find excellent resources like all of you at Math Munch! :-)
p.s. Just ordered a special set of stars from Paul — can’t wait to see what happens when we get to play with them…and the extra pieces.
Wow! This has some great implications for the classroom based on just playing around and seeing what patterns occur… Thanks so much!
Yeah, and cultivating authentic occasions for play in a classroom is tough, because classroom time is scarce and therefore precious. What’s the payoff to play? Sometimes nothing at all. But other times, the payoff is the only payoff that really ever matters.
So that’s what (for instance) free-choice time is for. But framing it so that it’s useful–and not framing it so much that it’s “useful”–is a tricky line to walk.
Thanks for reading! Excited to hear the results of your own playful patterning.
This is great, Justin!
Hey! How are ya? Glad you liked it.